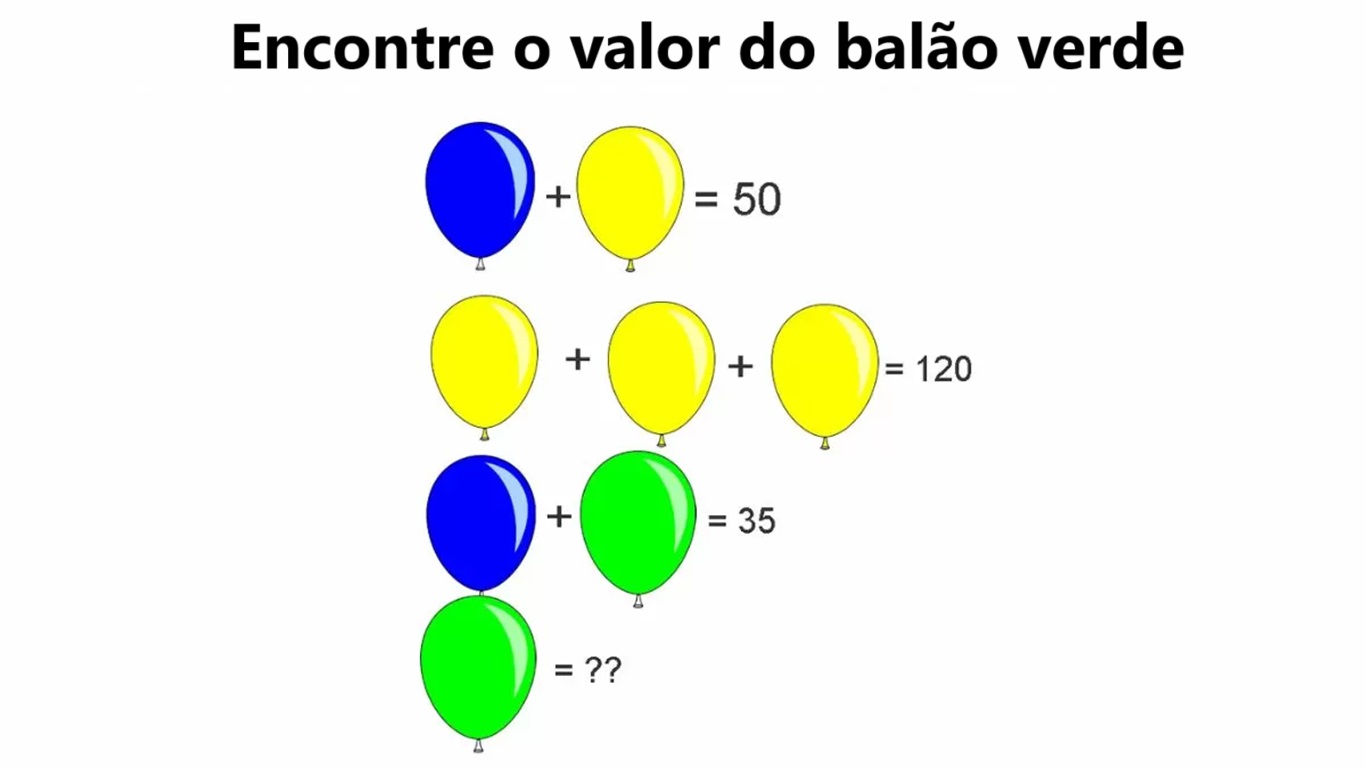
Charadas de matemática que vão ajudar no desenvolvimento do seu raciocínio lógico!
O raciocínio lógico é uma habilidade essencial que pode ser aprimorada de maneira divertida e desafiadora através de charadas matemáticas. […]


O raciocínio lógico é uma habilidade essencial que pode ser aprimorada de maneira divertida e desafiadora através de charadas matemáticas. Essas pequenas questões não apenas testam nosso conhecimento numérico, mas também nos fazem pensar “fora da caixa”, estimulando nossa criatividade e capacidade de resolver problemas.
Prepare-se! Vamos desafiar sua mente com enigmas que vão desde simples contagens até problemas mais complexos que exigirão um pouco mais de reflexão. Lembre-se: o objetivo não é apenas chegar à resposta certa, mas sim entender o processo de raciocínio por trás de cada charada.
Ao longo do texto, você encontrará uma variedade de questões que abordam diferentes aspectos da matemática, como aritmética, geometria e até mesmo um pouco de álgebra. Algumas charadas são mais diretas, enquanto outras podem conter pegadinhas que testarão sua atenção aos detalhes. Não se preocupe se não conseguir resolver todas de primeira – o importante é se divertir e aprender com cada desafio.
Então, pegue um papel e uma caneta, prepare sua mente e vamos começar esta aventura matemática!
Charadas de contagem e observação
Veja a seguir, charadas que testam sua habilidade de contar e observar detalhes importantes. Estas questões podem parecer simples à primeira vista, mas exigem atenção redobrada para não cair em armadilhas.
O Mistério das Casas na Rua
Uma senhora, durante sua caminhada vespertina, contou 20 casas à sua direita. No retorno, ela contabilizou 20 casas à sua esquerda. Quantas residências ela avistou no total?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Esta charada nos faz refletir sobre perspectiva e posicionamento. À primeira vista, poderíamos pensar que a resposta é 40 casas, somando as 20 de cada lado. No entanto, devemos considerar que a senhora está caminhando pela mesma rua, apenas em direções opostas. Portanto, as casas contadas na ida são as mesmas da volta, vistas do outro lado da rua. A resposta correta é 20 casas no total.
A Formação dos Patos
Imagine a seguinte situação: há um pato entre dois patos, um pato atrás de um pato e um pato na frente de outro pato. De quantos patos estamos falando?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Esta charada brinca com nossa percepção espacial. Podemos ser tentados a pensar que estamos falando de cinco patos, já que mencionamos um pato entre dois, um atrás de um e um na frente de outro. No entanto, se analisarmos com mais cuidado, perceberemos que estamos falando apenas de três patos.
A situação descrita pode ser visualizada da seguinte maneira: temos um pato no meio, com um pato à sua esquerda e outro à sua direita. Além disso, há um pato atrás do pato da esquerda e um pato na frente do pato da direita. Portanto, a resposta correta é três patos.
O Número Escondido
Em um jogo de adivinhação, você recebe a seguinte dica: “Estou pensando em um número entre 1 e 100. Esse número é divisível por 3, mas não é divisível por 4.” Qual é o número que estou pensando?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Para resolver essa charada, precisamos encontrar um número que seja divisível por 3, mas não seja divisível por 4. Podemos começar listando os múltiplos de 3 entre 1 e 100: 3, 6, 9, 12, 15, … No entanto, precisamos encontrar um número que não seja divisível por 4.
Ao analisar os múltiplos de 3, percebemos que alguns deles também são divisíveis por 4, como 12 e 24. Portanto, devemos procurar um número que seja divisível apenas por 3. O número correto é 9, pois é divisível por 3, mas não é divisível por 4.
Os Números Mágicos
Em uma mágica, um mágico pede para você escolher qualquer número de 1 a 10. Em seguida, ele faz alguns cálculos e revela o resultado. Surpreendentemente, o mágico sempre acerta o número que você escolheu. Como ele faz isso?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Essa charada envolve um truque matemático simples, mas eficaz. O truque está no cálculo feito pelo mágico. Ele pede para você multiplicar o número escolhido por 2, somar 5 ao resultado, multiplicar por 50 e, em seguida, adicionar 1769. Depois de realizar essas operações, o mágico revela o resultado.
Independentemente do número que você escolher, o resultado final sempre será 1769. Isso ocorre porque, ao analisar as operações, percebemos que multiplicar por 2 e somar 5 é o mesmo que multiplicar por 2 e adicionar 10. Em seguida, multiplicar por 50 é o mesmo que multiplicar por 100 e dividir por 2. Portanto, o resultado final será sempre 100 vezes o número escolhido, mais 1769.
Essas charadas de contagem e observação mostram como pequenos detalhes podem fazer toda a diferença na resolução de problemas matemáticos. Ao prestar atenção aos detalhes e analisar cuidadosamente as informações fornecidas, podemos encontrar as respostas corretas, mesmo quando parecem óbvias à primeira vista.
Charadas de Lógica e Raciocínio
Nesta seção, apresentaremos charadas que testam sua capacidade de raciocínio lógico e dedução. Essas questões exigem que você pense além do óbvio e encontre soluções criativas para os problemas apresentados.
O Relógio que Atrasa
Você tem um relógio que está atrasado em 6 minutos. No entanto, você precisa saber a hora exata, mas só tem um relógio normal que funciona corretamente. Como você pode descobrir a hora certa usando apenas esses dois relógios?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Essa charada nos desafia a encontrar uma solução criativa para descobrir a hora exata. A estratégia é simples: ajuste o relógio atrasado para que ele mostre a hora atual, acrescentando os 6 minutos que ele está atrasado. Em seguida, compare as horas mostradas pelos dois relógios. A diferença entre eles será exatamente de 6 minutos, permitindo que você determine a hora correta.
O Desafio das Cores
Em uma cidade, existem três casas, cada uma de uma cor diferente: vermelha, azul e verde. Em cada casa, mora uma pessoa com uma nacionalidade diferente: brasileiro, italiano e espanhol. Cada pessoa tem um animal de estimação diferente: cachorro, gato e pássaro. Além disso, cada pessoa gosta de uma bebida diferente: café, chá e suco.
Com base nas seguintes dicas, você consegue descobrir qual é a cor da casa de cada pessoa, a sua nacionalidade, o animal de estimação que ela tem e a bebida que ela gosta?
- O brasileiro mora na casa vermelha.
- O italiano tem um pássaro como animal de estimação.
- O dono da casa verde bebe café.
- O espanhol mora na primeira casa.
- O dono da casa do meio bebe chá.
- A casa azul fica ao lado da casa onde mora o dono do pássaro.
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Essa charada envolve a criação de uma tabela ou diagrama para organizar as informações e deduzir as respostas corretas. Ao analisar as dicas, podemos começar preenchendo algumas informações:
- O espanhol mora na primeira casa.
- O brasileiro mora na casa vermelha.
- O dono da casa verde bebe café.
Agora, usando a dica de que a casa azul fica ao lado da casa do dono do pássaro, podemos deduzir que a casa azul não pode ser a primeira nem a última. Portanto, a casa azul deve ser a do meio.
Continuando a análise das dicas, concluímos que o italiano tem um pássaro como animal de estimação e, portanto, deve morar na casa azul. O dono da casa verde bebe café, então o brasileiro não pode ser o dono da casa verde. Portanto, o brasileiro deve morar na casa vermelha.
Resta apenas a casa verde para o espanhol, que deve ter um gato como animal de estimação. Portanto, o italiano deve morar na casa azul e ter um pássaro, enquanto o espanhol deve morar na casa verde e ter um gato.
Com base nessas deduções, podemos concluir que:
- O brasileiro mora na casa vermelha, tem um cachorro e gosta de suco.
- O italiano mora na casa azul, tem um pássaro e gosta de chá.
- O espanhol mora na casa verde, tem um gato e gosta de café.
Essa charada mostra como o raciocínio lógico e a dedução podem nos ajudar a encontrar respostas precisas, mesmo quando as informações parecem complexas. Ao analisar cuidadosamente as dicas e fazer conexões entre elas, podemos chegar a uma solução correta.

Charadas de Matemática e Geometria
Essas charadas exigem que você aplique seus conhecimentos numéricos e espaciais para resolver os problemas propostos.
A Lógica das Idades
Três irmãos estão discutindo sobre suas idades. O mais velho diz: “Minha idade é o triplo da idade do mais novo.” O irmão do meio responde: “E a minha idade é o dobro da idade do mais novo.” O mais novo, por sua vez, diz: “E a minha idade é a metade da idade do mais velho.” Se somarmos as idades dos três irmãos, obtemos 30 anos. Qual é a idade de cada um?
Agora é com você! Tente resolver esta charada e em seguida, descubra qual é a resposta.
Essa charada envolve a criação de um sistema de equações para resolver o problema. Vamos chamar as idades do mais novo, do irmão do meio e do mais velho de x, y e z, respectivamente. Com base nas informações fornecidas, podemos escrever as seguintes equações:
- z = 3x (a idade do mais velho é o triplo da idade do mais novo)
- y = 2x (a idade do irmão do meio é o dobro da idade do mais novo)
- x = z/2 (a idade do mais novo é a metade da idade do mais velho)
Também sabemos que a soma das idades é igual a 30:
x + y + z = 30
Agora, podemos substituir as equações 1, 2 e 3 na equação da soma das idades:
x + 2x + 3x = 30 6x = 30 x = 5
Substituindo o valor de x nas equações 1, 2 e 3, encontramos as idades dos irmãos:
x = 5 (idade do mais novo) y = 2x = 2(5) = 10 (idade do irmão do meio) z = 3x = 3(5) = 15 (idade do mais velho)
Portanto, as idades dos três irmãos são 5, 10 e 15 anos, respectivamente.
What's Your Reaction?